В магазине стоят два платежных автомата. Каждый из них может...

Задание:

В магазине стоят два платежных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.

Решение:

Здесь удобно сначала найти вероятность события «оба автомата неисправны», противоположного событию из условия задачи. Пусть

А={1-ый автомат неисправен}
В={2-ой автомат неисправен}
По условию Р(А) = Р(В) = 0,05.
Событие «оба автомата неисправны» − это А∩В.
По формуле умножения вероятностей, его вероятность равна Р(А∩В) = Р(А)∙ Р(В) = 0,05 ∙ 0,05 = 0,0025. Значит,

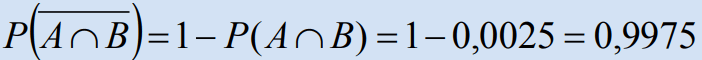
Ответ: 0,9975