В правильной треугольной пирамиде SABC...
Категория: Задание 8 ЕГЭ по математике (Стереометрия)
Задание:
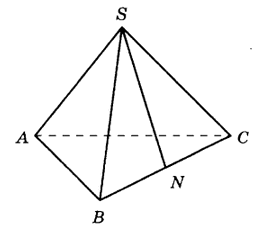
В правильной треугольной пирамиде SABC N - середина ребра BC, S - вершина. Известно, что SN = 6, а площадь боковой поверхности равна 72. Найдите длину отрезка AB.
Решение:
* Площадь боковой поверхности правильной пирамиды равен:
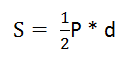
* P - периметр основания пирамиды; d - апофема (высота боковой грани)
* По условию задачи d = SN = 6
* Так как пирамида правильная, значит в основании равносторонний треугольник, следовательно:
AB = BC = AC = X
P = x + x + x = 3x
* Подставляем в формулу:
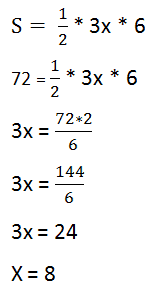
* AB = x = 8
Ответ: 8