Биссектриса тупого угла параллелограмма делит...
Категория: Задание 6 ЕГЭ по математике (Планиметрия)
Задание:
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 6 : 7, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 190.
Решение:
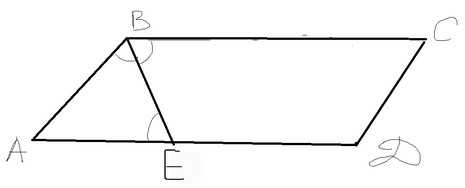
* Обозначим одну часть за x(икс), тогда AE = 6x, ED = 7x, а большая сторона = AD = 6x + 7x = 13x
* Угол ABE = углу CBE - биссектриса делит угол пополам. =>
Угол ABE = углу BEA = углу CBE = углу DEB - накрест лежащие углы =>
Треугольник ABE - равнобедренный (углы при основании равны).
AB = AE = CD = 6x.
* Перимитр ABCD = AB + BC + CD + AD = 6x + 13x + 6x + 13x = 38x
190 = 38x
x = 5
* Большая сторона = 13x = 13 * 5 = 65
Ответ: 65
