Дана правильная четырёхугольная пирамида KMNPQ...

Задание:

Дана правильная четырёхугольная пирамида KMNPQ со стороной основания MNPQ, равной 6 , и боковым ребром З√26.

а) Постройте сечение пирамиды плоскостью, проходящей через прямую NF параллельно диагонали МР, если точка F — середина ребра МК.

б) Найдите величину угла между плоскостью сечения и плоскостью КМР.

Решение:

а) Пусть KO — высота пирамиды, F — середина MK; FE || MP (в плоскости P KM). Так как FE — средняя линия ΔPKM, то FE = MP/2.

Построим сечение пирамиды плоскостью, проходящей через NF и параллельной MP, то есть плоскостью NFE. L — точка пересечения EF и KO. Так как точки L и N принадлежат искомому сечению и лежат в плоскости KQN, то точка T, полученная как пересечение LN и KQ, является также точкой пересечения искомого сечения и ребра KQ. NETF — искомое сечение.

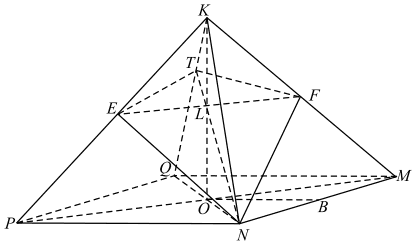
б) Плоскости NFE и MP K пересекаются по прямой FE. Значит, угол между этими плоскостями равен линейному углу двугранного угла OFEN, построим его: LO ⊥ MP, MP k FE, следовательно, LO ⊥ FE; ΔNFE — равнобедренный (NE = NF как соответствующие медианы равных треугольников KPN и KMN), NL — его медиана (EL = LF, так как PO = OM, а ΔKEF ∼ ΔKPM). Отсюда NL ⊥ FE и ∠NLO — искомый.

ON = 1/2*QN = 1/2*MN√2 = 3√2.

ΔKON — прямоугольный.

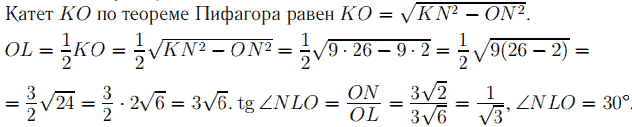
Ответ: 30.