В прямоугольном параллелепипеде ABCDA1B1C1D1...

Задание:

В прямоугольном параллелепипеде ABCDA₁B₁C₁D₁ стороны осно­ваний АВ и ВС равны соответственно 6 и 4, а боковое ребро равно 3. На ребре А₁В₁ отмечена точка М , а на луче ВС — точка F , причём А₁М = МВ₁ и BF = АВ. Плоскость AMF пересекает ребро СС₁ в точ­ке N.

а) Докажите, что CN : C₁N = 2 : 1.

б) Найдите расстояние от точки В до плоскости сечения.

Решение:

а) 1. Построим сечение параллелепипеда плоскостью AMF (см. рис.). Отрезок AF пересекает ребро DC в точке P.

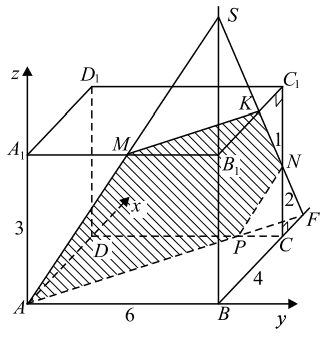
В плоскости ABB₁ проведём лучи AM и BB₁, AM пересекает BB₁ в точке S. В плоскости BCC₁ проведём отрезок SF, SF пересекает B₁C₁ в точке K, а CC₁ в точке N. Пятиугольник AMKNP — искомое сечение.

AB ‖ MB₁, AB = 2MB₁, значит, MB₁ — средняя линия ΔSBA, отсюда MB₁ = 1/2 * A₁B₁ = 3. B₁K ‖ BC, BB₁ = B₁S, отсюда B₁K — средняя линия ΔSBF, B₁K = 1/2 * BF = 3, тогда KC₁ = 1, CF = 2. ΔFCN ∼ ΔKC₁N по первому признаку подобия (∠C = ∠C1 = 90◦ , ∠1 = ∠2 как вертикальные). Из подобия следует: CN/C₁N = CF/C₁K = 2/1 . Что и требовалось доказать.

б) 1. Введём прямоугольную систему координат, как показано на рисунке.

2. В этой системе координат найдём координаты нужных нам точек A(0; 0; 0), M(0; 3; 3), F(6; 6; 0), B(0; 6; 0).

3. Найдём координаты двух неколлинеарных векторов, лежащих в плоскости AMF: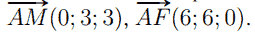

4. Обозначим через 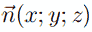 — вектор нормали к плоскости AMF, координаты которого нам нужно найти. Искомый вектор перпендикулярен векторам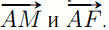 

5. Получим систему уравнений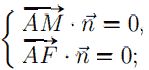  

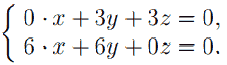
При x = 1 эта система примет вид: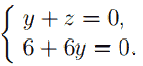 

Её решение: y = −1, z = 1.

Имеем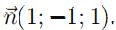  

x − y + z + d = 0.

С учётом того, что плоскость проходит через начало координат, d = 0 и уравнение примет вид: x − y + z = 0.

Искомое расстояние от точки B(0; 6; 0) найдём по формуле

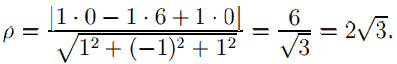
Ответ: 2√3.