В правильной четырёхугольной призме MNPQM1N1P1...

Задание:

В правильной четырёхугольной призме MNPQM₁N₁P₁Q₁ сторона основания равна 11, а боковое ребро равно 15. На рёбрах M₁Q₁, M₁N₁ и PQ взяты точки X , Y, Z, соответственно так, что Q₁X = N₁Y = QZ = 5.

а) Пусть С — точка пересечения плоскости XYZ с ребром PN . Докажите, что XYZC — прямоугольник.

б) Найдите площадь сечения призмы плоскостью XYZ.

Решение:

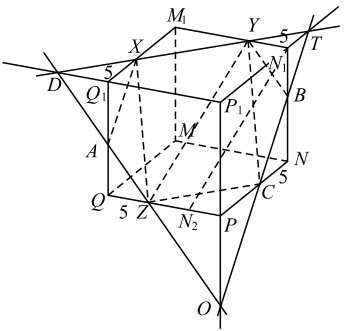
а) Найдём положение точки C. Эта точка пересечения плоскости XYZ и ребра PN, лежащего в плоскости MNPQ (см. рис.). Плоскость MNPQ параллельна плоскости M₁N₁P₁Q₁, в которой лежит отрезок XY . Плоскость XYZ пересекает параллельные плоскости MNPQ и M₁N₁P₁Q₁ по параллельным прямым, отсюда XY || ZC. Прямоугольные треугольники YXM₁ и ZCP равны по катету и острому углу (M₁Y = PZ = 6 и ∠M₁YX = ∠PZC как острые с соответственно параллельными сторонами). Чтобы доказать, что четырёхугольник XYCZ — прямоугольник, найдём длины его сторон и диагонали.

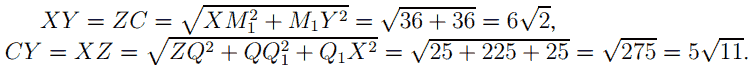Противоположные стороны четырёхугольника попарно равны, значит, это параллелограмм. Проведём N₁N₂ || YZ, тогда

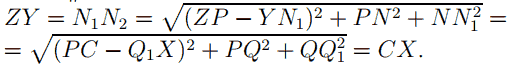
Диагонали параллелограмма равны, следовательно, FKLP — прямоугольник.

б) Пусть D и T — точки пересечения прямой XY и прямых Q₁P₁ и P₁N₁. Проведём прямые DZ и TC, они пересекут рёбра QQ₁ и NN₁ в точках A и B соответственно (см. рис.). D — точка пересечения прямых XY и AZ. Тогда DQ₁ = Q₁X = QZ. Легко доказать, что треугольники DQ₁A и ZQA равны и AQ = AQ₁. Поэтому прямая DZ, а значит, и плоскость XYZ пересекают ребро QQ₁ в его середине — точке A. Аналогично плоскость XYZ пересекает ребро NN₁ в его середине — точке B.

В диагональном сечении QQ₁N₁N, которое является прямоугольником, отрезок AB — средняя линия. В прямоугольнике QABN противоположные стороны равны: AB = QN = 11√ 2.

Сечение XYBCZA состоит из двух равных трапеций AXYB и AZCB, причём мы доказали, что ZX ⊥ XY и ZX ⊥ ZC. Высота каждой из этих трапеций равна ZX / 2 = 5 √11 / 2 .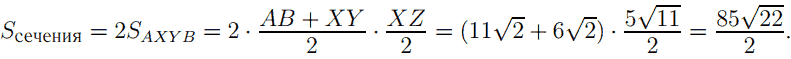

Ответ: 85√22 / 2 .