Сечением прямоугольного параллелепипеда ABCDA...

Задание:

Сечением прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ плоскостью α, содержащей прямую BD₁ и параллельной прямой АС, является ромб.

а) Докажите, что грань ABCD – квадрат.

б) Найдите угол между плоскостями α и BCC₁, если AA₁ = 6, AB = 4.

Решение:

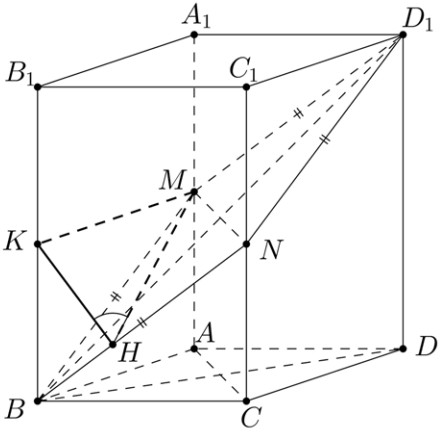
а) Диагонали ромба перпендикулярны, проекциями этих диагоналей на плоскость ABCD являются диагонали прямоугольника ABCD, которые также должны быть перпендикулярны. Значит ABCD – квадрат.

б) Из доказанного следует, что треугольники BCN, BAM, D₁A₁M, D₁C₁N равны по катету и гипотенузе, откуда M и N являются серединами рёбер AA₁ и CC₁ соответственно.

Проведем перпендикуляр из M к плоскости BCC₁ – MK. Из точки K проведем перпендикуляр к BN, получим точку Н. Угол MHK – искомый линейный угол между плоскостями.

Из треугольника BKN с катетами 3 и 4 находим высоту КН = 12/5.

По построению КМ = 4, поэтому угол MHK найдется:

∠ МНК = arctg MK/KH = arctg 5/3.

Ответ: а) ч.т.д.; б) arctg 5/3.