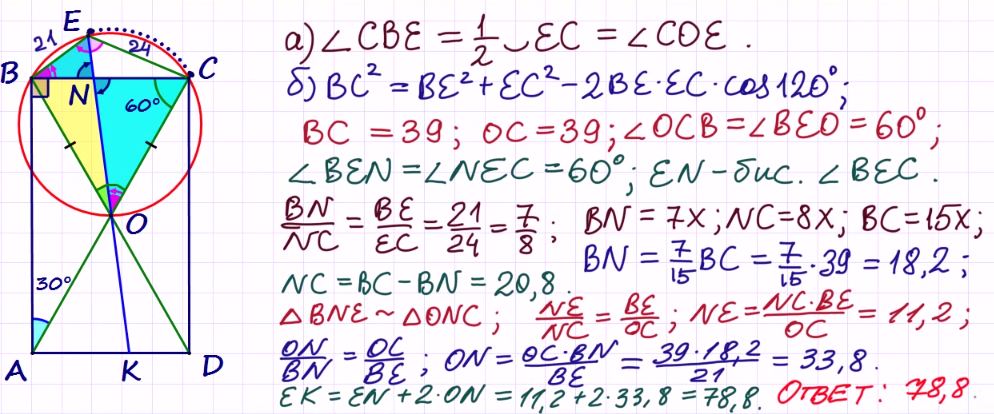Диагональ AC прямоугольника ABCD с центром O..

Задание:

Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30 градусов. Точка E лежит вне прямоугольника, причём ∠BEC=120 градусов. а) Докажите, что ∠CBE = ∠COE. б) Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, если известно, что BE=21 и CE=24.

Ответ:  a) ∠CBE = 1/2⋃EC = ∠COE

                б) EK = 78,8

Краткое решение: