В треугольнике ABC точки А1, В1 и С1 – середины...

Задание:

В треугольнике ABC точки А₁, В₁ и С₁ – середины сторон ВС, АС и АВ соответственно, АН – высота, ∠ ВАС = 60º, ∠ВСА = 45º.

а) Докажите, что точки А₁, В₁, С₁ и Н лежат на одной окружности.

б) Найдите А₁Н ,если ВС = 2√3.

Решение:

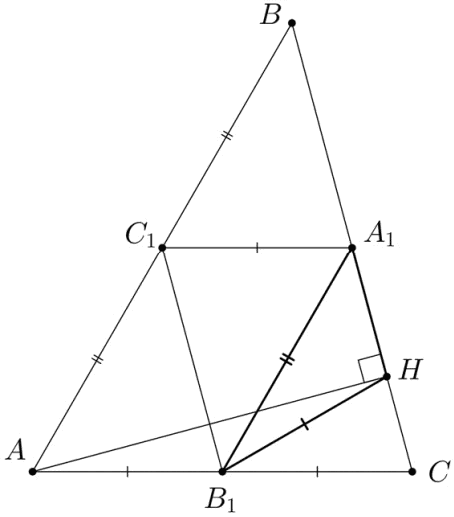
а) В₁Н – медиана прямоугольного треугольника АНС, поэтому

АВ₁ = В₁С = В₁Н,   ∠В₁СН = ∠СНВ₁,   ∠АНВ₁ = 15º,   ∠СВ₁Н = 30º.

Из равенства треугольников А₁В₁С₁, АС₁В₁, В₁А₁С, С₁ВА₁ следует ∠А₁С₁В₁ + ∠А₁НВ₁ = 75º + 90º + 15º = 180º.

Значит около четырехугольника ܣଵܤܪଵܥଵ можно описать окружность.

б) По теореме синусов находим: 

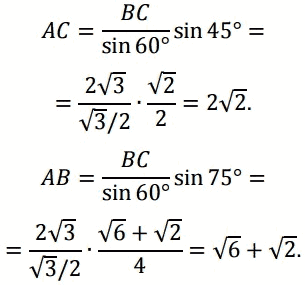
Тогда,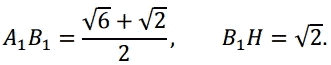 

По теореме косинусов для треугольника А₁В₁Н:

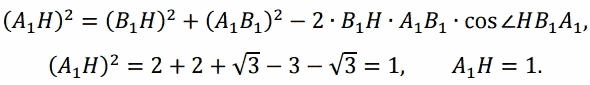
Ответ: а) ч.т.д.; б) 1.