Две окружности касаются внешним образом в точке K...

Задание:

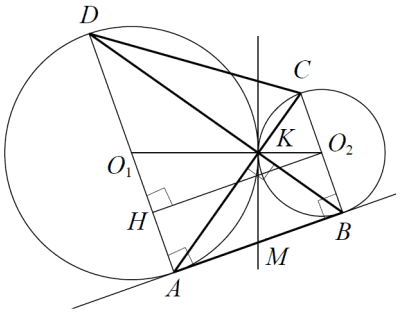
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке А, а второй – в точке В. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке С.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.

Решение:

а) Обозначим центры окружностей O₁ и O₂ соответственно. Пусть общая касательная, проведённая к окружностям в точке K, пересекает AB в точке M. По свойству касательных, проведенных из одной точки, AM = KM и KM = BM. Треугольник AKB, у которого медиана равна половине стороны, к которой она проведена, прямоугольный.
Вписанный угол AKD прямой, поэтому он опирается на диаметр AD. Значит, AD⊥AB. Аналогично, получаем, что BC⊥AB. Следовательно, прямые AD и BC параллельны.

б) Пусть, для определенности, первая окружность имеет радиус 4, а вторая – радиус 1.

Треугольники ВKC и AKD подобны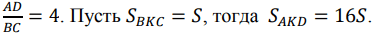 

У треугольников AKD и AKB общая высота, следовательно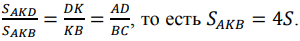 

Аналогично, 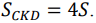 Площадь трапеции ABCD равна 25S. Вычислим площадь трапеции ABCD. Проведём к АD перпендикуляр O₂H, равный высоте трапеции, и найдем его из прямоугольного треугольника О₂НО₁:

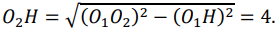
Тогда,

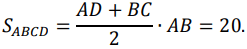
Следовательно, 25S = 20, откуда S = 0,8 и S_AKB = 4S = 3.2.

Ответ: 3.2.