Две окружности различных радиусов касаются друг...

Задание:

Две окружности различных радиусов касаются друг друга внешним образом. Их общие касательные, не проходящие через точку касания окружностей, пересекаются в точке О. При этом одна из касательных касается окружностей в точках А и С, считая от точки О, а другая, — соответственно в точках В и D.

а) Докажите, что прямая CD перпендикулярна биссектрисе угла, образованного указанными касательными.

б) Найдите расстояние от середины отрезка CD до точки А, если радиусы окружностей равны 3 и 9.

Решение:

а) Рассмотрим рисунок. На нём O₁ и O₂ — центры окружностей (по свойству вписанной в угол окружности точки O₁ и O₂ лежат на биссектрисе ∠AOB), K и T — точки пересечения соответственно AB и CD c биссектрисой. O₁A и O₂C — радиусы окружностей, перпендикулярные касательной AC.

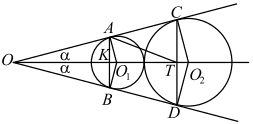
ΔO₂CO = ΔO₂DO по общей гипотенузе и острому углу, поэтому OC = OD. Таким образом, треугольник COD является равнобедренным, и биссектриса OT угла O является высотой и медианой, поэтому точка T является серединой отрезка CD. Это и означает, что прямая CD перпендикулярна биссектрисе ∠COD.

б) Пусть ∠COO₂ равен α. Проведём через O₁ прямую O₁L, параллельную AC.

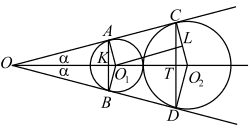
Тогда по свойству соответственных углов при параллельных прямых OC и O₁L и секущей OO₂ ∠LO₁O₂ = α. Но O₁O₂ = 3 + 9 = 12, а LO₂ = 9 − 3 = 6. Поэтому sin α = LO₂ O₁O₂ = 6/12 = 1/2. Так как α — острый угол, то α = 300 , cos α = √3 / 2 , tg α = 1 / √3.

Заметим, что AO₁ / OA = tg α = 1 / √3, OA = AO₁ / tg α = 3 / 1 / √3 = 3√3. Аналогично CO₂ / OC = tg α = 1 / √3, OC = CO₂ / tg α = 9 / 1 / √3 = 9√3, OT = OC * cos α = 9√3 * √3/2 = 27/2.

По теореме косинусов в ΔAOT 

AT² = OA² + OT² − 2 * OA * OT * cos α = 27 + 729/4 − 2 * 3√3 * 27/2 * √3/2 = 351 / 4 , AT = √351 / 2 = 3√39 / 2.

Ответ: 3√39 / 2.