Найдите площадь прямоугольного треугольника...

Задание:

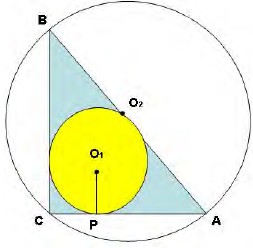
Найдите площадь прямоугольного треугольника, если радиусы вписанной в него и описанной около него окружностей равны соответственно 2м и 5м.

Решение:

ОСНОВНЫЕ ФОРМУЛЫ

• Центр описанной окружности – середина гипотенузы;
• радиус вписанной окружности;
• Свойства касательных;
• теорема Пифагора;
• площадь треугольника;

S = 0,5 * a * b; с = 10, CP = PO₁ = 2.
Пусть CA = 2 + x, CB =y + 2, тогда AB = x + y = 10.
(2 + x)² + (2 + y)² = 100.

4 + 4x + x² + 4 + 4y + y² = 100;
x² + y² = 52;
100 – 20x + x² + x² = 52;
2x² - 20x + 48 = 0;
x² - 10x + 24 = 0;
x₁ = 6; x₂ = 4, тогда у = 6 или у = 4.
АС = a = 8, СВ = b = 6,
S = 0,5 a · b = 0,5·8· 6 = 24

Ответ: 24