Окружность, вписанная в остроугольный треугольни...

Задание:

Окружность, вписанная в остроугольный треугольник АВС, касается сторон АВ и АС в точках М и N.

а) Докажите что центр окружности, вписанной в треугольник AMN, лежит на окружности, вписанной в треугольник АВС.

б) Найдите расстояние между центрами этих окружностей, если АВ = CN = 10, BM = 6, sin A = 4√3 / 7.

Решение:

а) Пусть точка O — центр вписанной окружности треугольника ABC. Тогда O лежит на биссектрисе угла A.

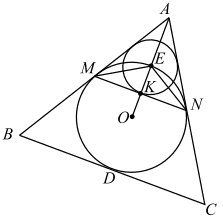
Биссектриса AO пересекает дугу MN в точке E, а отрезок MN в точке K. AM = AN как отрезки касательных, проведённых к окружности из одной точки, отсюда ΔMAN — равнобедренный, значит, биссектриса AK является медианой и высотой. ΔEKM = ΔEKN по двум катетам (MK = KN, EK — общая сторона). Из равенства треугольников следует: EM = EN, а так как равные хорды стягивают равные дуги, то ◡ EM = ◡ EN.

Докажем, что точка E — центр вписанной окружности треугольника MAN. ∠ANE = 1/2 ◡ NE как угол между касательной AN и хордой EN.

∠MNE = 1 2 ◡ ME как вписанный. ◡ NE = ◡ ME, значит, ∠ANE = ∠MNE, тогда NE — биссектриса угла ANM. Отсюда следует, что E — точка пересечения биссектрис углов A и N треугольника AMN, следовательно, E — центр вписанной окружности.

б) По доказанному выше центр вписанной окружности треугольника MAN — точка E — лежит на вписанной окружности треугольника ABC, следовательно, искомое расстояние равно радиусу вписанной окружности треугольника ABC.

Из формулы S_ABC = 1/2 * P_ABC * r найдём радиус r = 2S_ABC / P_ABC.

Задача сводится к нахождению площади и периметра треугольника ABC. S_ABC = 1/2 * AB * AC * sin A.

Найдём AC.

AM = AB − BM = 10 − 6 = 4, AN = AM = 4,

AC = AN + CN = 4 + 10 = 14.

S_ABC = 1/2 * 10 * 14 * 4√3/7 = 40√3.

В ΔABC по теореме косинусов BC² = AB² + AC² − 2AB * AC * cos A.

По условию ΔABC остроугольный, поэтому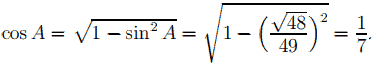 

BC² = 10² + 14² − 2 * 10 * 14 * 1/7 , BC² = 256.

BC = 16, P_ABC = 10 + 14 + 16 = 40, r = (2 * 40√3) / 40 = 2√3.

Расстояние между центрами OE = 2√3.

Ответ: 2√3.