Окружность, вписанная в остроугольный треугольник...

Задание:

Окружность, вписанная в остроугольный треугольник АВС, касается сторон ВА и ВС в точках М и N.

а) Докажите, что центр окружности, вписанной в треугольник BMN , лежит на окружности, вписанной в треугольник АВС.

б) Найдите расстояние между центрами этих окружностей, если АВ = 10, AC = 12, sin a = √7/4.

Решение:

а) Пусть точка O — центр окружности, вписанной в ΔABC. Биссектриса BD пересекает дугу MN в точке K, а отрезок MN в точке E. BM = BN как отрезки касательных, проведённых к окружности из одной точки, отсюда ΔMBN — равнобедренный, значит, биссектриса BE — медиана и высота. ΔKME = ΔKNE по двум катетам (ME = NE, KE — общая сторона). Из равенства треугольников следует: MK = NK, а так как равные хорды стягивают равные дуги, то ◡ KM = ◡ KN. Докажем, что K — центр вписанной окружности треугольника ΔMBN.

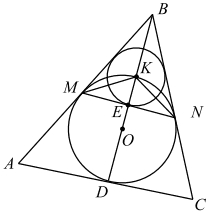
∠KMN = 1/2 ◡ NK как вписанный, ∠KMB = 1/2 ◡ MK как угол между касательной BM и хордой KM. ◡ MK = ◡ NK, значит, ∠KMN = ∠KMB, тогда MK — биссектриса угла NMB. Отсюда следует, что K — точка пересечения BE и MK, то есть точка пересечения биссектрис 4BMN, а значит, центр вписанной окружности.

б) По доказанному в пункте а) центр вписанной окружности △BMN лежит на вписанной окружности △ABC, следовательно, искомое расстояние равно радиусу вписанной окружности △ABC.

Из формулы S_ABC = p * r следует, что r = S_ABC / p , где r — радиус вписанной окружности, p — полупериметр.

1. Найдём площадь 4ABC:

SABC = 1/2 * AB * AC * sin A, S_ABC = 1/2 * 10 * 12 * √7/4 = 15√7.

В △ABC по теореме косинусов BC² = AB² + AC² − 2AB * AC * cos A.

По условию △ABC остроугольный, поэтому

cos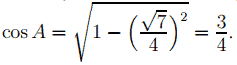

BC² = 10² + 12² − 2 * 10 * 12 * 3 4 , BC = 8.

2. Найдём p = P_ABC / 2 = (10 + 12 + 8) / 2 = 15.

3. Расстояние между центрами окружностей OK = r = 15√7 / 15 = √7.

Ответ: √7.