Основания равнобедренной трапеции равны 20 и 50...
Категория: Задание 6 ЕГЭ по математике (Планиметрия)
Задание:
Основания равнобедренной трапеции равны 20 и 50, а её боковые стороны равны 17. Найдите площадь трапеции.
Решение:
Рассмотрим равнобедренную трапецию ABCD, в которой BC = 20, AD = 50 — основания, AB = CD = 17 (см. рис.). Проведём высоты CP и BH. BCPH — прямоугольник, BC = PH = 20. Прямоугольные треугольники ABH и DCP равны по гипотенузе и катету (AB = CD, BH = CP), и тогда AH = PD = (50 − 20) : 2 = 15.
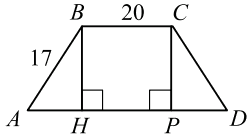
Треугольник ABH прямоугольный, BH = √(172 − 152) = 8. Площадь трапеции равна S = (BC + AD) / 2 · BH = (20 + 50) / 2 · 8 = 280.
Ответ: 280.