В правильной треугольной призме АВСА1В1С1 стор...

Задание:

В правильной треугольной призме АВСА₁В₁С₁ сторона основания АВ равна 8√3, а боковое ребро АА₁ = 6 . На ребре В₁С₁ отмечена точка L так, что В₁L = 2√3. Точки К и М — середины рёбер АВ и А₁С₁ соответственно. Плоскость γ параллельна прямой АС и содержит точки К и L.

а) Докажите, что прямая ВМ перпендикулярна плоскости γ.

б) Найдите объём пирамиды, вершина которой — точка М , а основание — сечение данной призмы плоскостью γ.

Решение:

а) 1. Построим сечение призмы плоскостью γ.

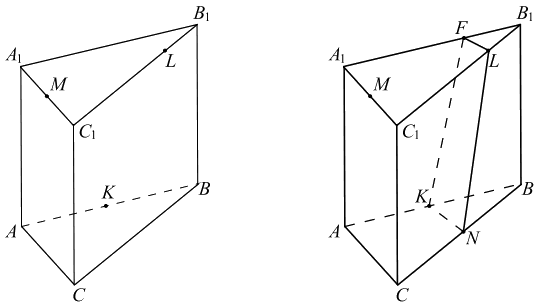
Плоскость ABC проходит через прямую AC, параллельную плоскости γ, и пересекает её (K — общая точка этих плоскостей), следовательно, линия пересечения этих плоскостей параллельна прямой AC. В плоскости ABC построим среднюю линию KN. Аналогично в плоскости A₁B₁C₁ проведём LF || A₁C₁. FKNL — сечение призмы плоскостью γ.

2. Докажем, что BM ⊥ γ.

Проведём MT || AA1. Плоскость BTM перпендикулярна прямой AC. Действительно, AC перпендикулярна двум пересекающимся прямым (MT, BT) плоскости BTM. Следовательно, BM ⊥ AC, значит, BM ⊥ KN.

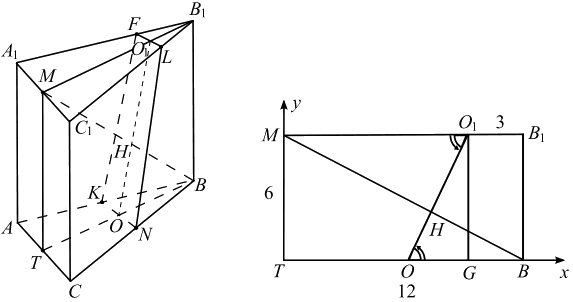
Докажем теперь, что MB ⊥ OO₁. Рассмотрим прямоугольник BTMB₁.

MT = 6, B₁O₁ = 3, BT = 12 (высоты правильных треугольников B₁FL и ABC соответственно). Введём систему координат и найдём скалярное произведение векторов .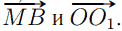

M(0; 6), B(12; 0), 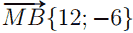; O(6; 0), O₁(9; 6) , .

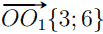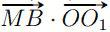 = 12 · 3 + (−6) · 6 = 0. Это означает, что векторы  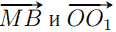перпендикулярны, следовательно, MB ⊥ OO₁. Итак, MB перпендикулярна двум пересекающимся прямым KN и OO₁ плоскости γ, а значит, MB ⊥ γ.

б) ΔMHO₁ ∼ ΔOO₁G как прямоугольные треугольники с равными острыми углами, ∠MO₁H = ∠GOO₁ как накрест лежащие при MB₁ || BT и секущей OO₁. Из этого следует, что MO₁/OO₁ = MH/O₁G , MO₁ = 9, O₁G = 6, OO₁ найдём по теореме Пифагора из прямоугольного треугольника OO₁G.

OO₁ =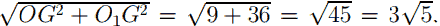  

9 · 6 = 3√5MH, откуда MH = 18√5 / 5 . MH — высота пирамиды MKNLF. Площадь равнобедренной трапеции KNLF с основаниями KN и LF и высотой OO₁ равна (KN + LF)/ 2 * OO₁. KN — средняя линия треугольника ABC, KN = 1/2 * AB = 4√3. LF — сторона правильного треугольника LB₁F (LF || A₁C₁), поэтому LF = LB₁ = 2√3.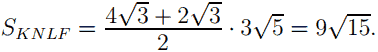  

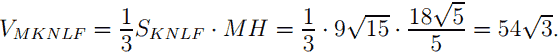
Ответ: б) 54√3.