Угол между биссектрисой и медианой прямоугольного...

Задание:

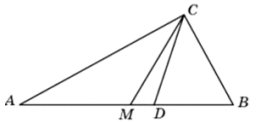
Угол между биссектрисой и медианой прямоугольного треугольника, проведёнными из вершины прямого угла, равен 14°. Найдите меньший угол прямоугольного треугольника.

Решение:

1) Угол C по условию задачи = 90°. Угол ACD = углу DCB = 90 / 2 = 45°, так как биссектриса CD делит угол пополам.
2) Угол MCD = 14° по условию = > Угол MCB = 14° + 45° = 59°.
3) Медиана в прямоугольном треугольнике проведённая из прямого угла к гипотенузе равна её половине => CM = MB, а значит треугольник CMB равнобедренный. Вспомним, что в равнобедренном треугольнике углы при основании равны, следовательно: Угол MCB = углу MBC = 59°.
4) Теперь рассмотрим весь треугольник ACB. Угол C = 90° по условию, угол B = 59° => угол A = 180° - угол C - угол B = 180° - 90° - 59° = 31°. 

Меньший угол - угол A = 31°.

Ответ: 31