В окружность с центром О вписан остроугольный треугольник...
Задание:
В окружность с центром О вписан остроугольный треугольник ABC, в котором проведена медиана BК , причём ∠KBC = ∠OCB.
а) Докажите, что точка О лежит на медиане ВК.
б) Найдите площадь треугольника АОВ, если ∠ABC = 60°, АВ = 4√3.
Решение:
а) Докажем, что точка O лежит на медиане BK.
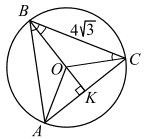
ΔBOC — равнобедренный (OB = OC как радиусы), следовательно, ∠OCB = ∠OBC (как углы при основании равнобедренного треугольника). По условию ∠KBC = ∠OCB, значит, ∠KBC = ∠OBC.
ΔABC — остроугольный, значит, O лежит внутри треугольника, K и O лежат по одну сторону от BC. В этом случае из равенства ∠KBC и ∠OBC следует, что точка O лежит на медиане BK.
б) ΔAOC — равнобедренный, так как AO = OC (как радиусы), OK — медиана, тогда OK — высота, отсюда BK — высота в ΔABC, BK — высота и медиана ΔABC, значит, он равнобедренный, AB = BC.
По условию ∠ABC = 60◦ , тогда ∠BAC = ∠BCA = 60◦ , AB = BC = AC = 4√3. ΔABC — правильный. ΔAOB = ΔBOC = ΔAOC (по трём сторонам),
SBOA = 1/3*SABC = 1/3 * AB2√3 /4 = (16 * 3√3) /12 = 4√3.
Ответ: 4√3.