В основании правильной треугольной призмы ABCA1B1C1...

Задание:

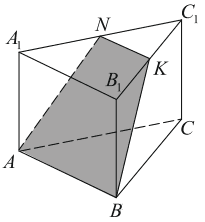
В основании правильной треугольной призмы ABCA₁B₁C₁ лежит треугольник со стороной 6. Высота призмы равна 4. Точка N — середина ребра A₁C₁.

а) Постройте сечение призмы плоскостью BAN.

б) Найдите периметр этого сечения.

Решение:

а) Проведём через точку N прямую, параллельную прямой AB, до пересечения с прямой B₁C₁ в точке K. Трапеция ABKN — искомое сечение. 

б) Имеем A₁N= 3, так как точка N — середина ребра A₁C₁ . Значит, 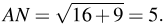Аналогично BK = 5.

Далее NK = 3 как средняя линия треугольника A₁B₁C₁ . Следовательно, искомый периметр сечения равен 6 + 5 + 5 + 3 = 19.

Ответ: 19.