В правильной четырёхугольной пирамиде SABCD ст...

Задание:

В правильной четырёхугольной пирамиде SABCD сторона основания АВ = 6, высота SO = 4. На апофеме ST грани BSC отмечена точка К так, что SK = 2. Плоскость γ параллельна прямой ВС и содержит точки K и D.

а) Докажите, что расстояние от точки С до плоскости γ равно расстоянию от точки В до плоскости γ.

б) Найдите объём пирамиды, вершина которой точка С, а основание — сечение данной пирамиды плоскостью γ.

Решение:

Построим сначала сечение пирамиды плоскостью γ.

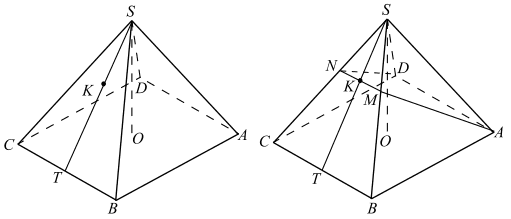
а) Плоскость γ пересекает плоскость SAD по прямой AD, а плоскость SBC — по прямой MN, проходящей через точку K, параллельной BC (если плоскость проходит через прямую, параллельную другой плоскости, и пересекает её, то линия пересечения параллельна это прямой). ADNM — сечение пирамиды плоскостью γ. ADNM — равнобедренная трапеция.

BC || γ, следовательно, любая точка, принадлежащая прямой BC, равноудалена от плоскости γ. Значит, расстояние от точки C до плоскости γ равно расстоянию от точки B до плоскости γ.

б) Так как расстояние от любой точки прямой BC до плоскости γ одно и то же, будем искать расстояние от точки T до плоскости γ, то есть нужно из точки T провести отрезок TH, перпендикулярный плоскости ADN, который равен высоте пирамиды CADNM.

Тогда V_CADNM = 1/3 * S_ADNM * TH. Точка K — середина отрезка MN, так как принадлежит апофеме ST. Обозначим через P середину отрезка AD, тогда KP ⊥ AD как высота равнобедренной трапеции ADNM, S_ADNM = (AD + MN) /  2 * PK.

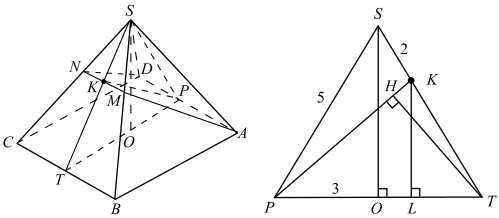
AD ⊥ PST, действительно, KP ⊥ AD и PT ⊥ AD, следовательно, достаточно построить отрезок TH ⊥ PK, так как тогда TH перпендикулярна двум пересекающимся прямым плоскости γ (AD и PK).

S_ΔPKT выразим двумя способами: 1/2 * TH * PK = 1/2 * PT * KL, откуда TH = (PT * KL) / PK. PT = 6. ST — гипотенуза прямоугольного треугольника SOT с катетами OT = 3, SO = 4, по теореме Пифагора ST = 5. KL найдём из подобия прямоугольных треугольников SOT и KLT с общим острым углом STO:

SO/KL = ST/KT = OT/LT ,  

4/KL = 5/3 ,  

KL = 12/5 ,  

3/LT = 5/3 ,  

LT = 9/5 ,  

OL = 3 − 9/5 = 6/5 .

PK найдём по теореме Пифагора из прямоугольного треугольника PKL:

PK² = PL² + LK² = (PO + OL)² + LK² ,

PK² = (3 + 6/5)² + (12/5)² = 585/25 , PK = √(585/5) = 3√65 / 5.

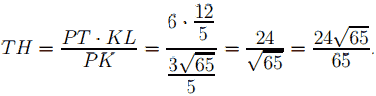
Основание MN равнобедренной трапеции найдём из подобия треугольников SMN и SBC, высоты которых SK = 2, ST = 5.

SK/ST = MN/BC , MN/6 = 2/5 , откуда, MN = 12/5.

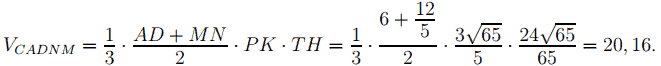
Ответ: 20,16.