В правильной четырёхугольной призме ABCDA1B1C1D1...

Задание:

В правильной четырёхугольной призме ABCDA₁B₁C₁D₁ сторона основания АВ = 4√2, боковое ребро АА₁ = 8, М середина ребра А₁В₁. На ребре DD₁ отмечена точка L так, что DL = 2. Плоскость 7 параллельна прямой А₁С₁ и содержит точки М и А.

а) Докажите, что прямая BL перпендикулярна плоскости γ.

б) Найдите объём пирамиды, вершина которой точка В, а основание — сечение данной пирамиды плоскостью γ.

Решение:

а) Построим сечение призмы плоскостью γ.

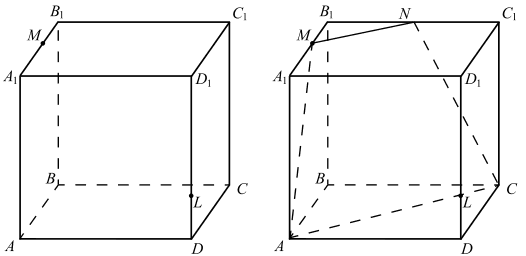
Плоскость γ пересекает плоскость ABC по прямой AC, а плоскость A₁B₁C₁ — по прямой MN (N — середина B₁C₁), проходящей через точку M, параллельной A₁C₁ (если плоскость проходит через прямую, параллельную другой плоскости, и пересекает её, то линия пересечения параллельна это прямой). AMNC — сечение пирамиды плоскостью γ. AMNC — равнобедренная трапеция. AMNC || A₁C₁.

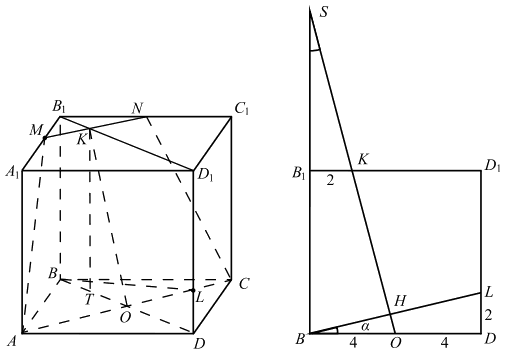
Рассмотрим диагональное сечение BB₁D₁D призмы ABCDA₁B₁C₁D₁. BB₁D₁D — квадрат, так как BB₁ = BD = 8. O — точка пересечения диагоналей AC и BD квадрата ABCD со стороной, равной 4√2, значит, AO = OC = 4. MN — средняя линия треугольника A₁B₁C₁, MK = KN, B₁K = 1/4*B₁D₁ = 2.

Пусть ∠DBL = α, тогда в прямоугольном треугольнике DBL ∠BLD = 90◦ − α. ΔSBO ∼ ΔB₁SK с коэффициентом подобия 2, следовательно, SB₁ = 8. ΔB₁SK = ΔDBL по двум катетам. Значит, ∠BSO = α, ∠BOS = 90◦ − α, ∠HOD = 180◦ − ∠HOB = 180 − (90◦ − α) = 90◦ + α. В выпуклом четырёхугольнике OHLD сумма углов равна 360◦ : ∠O + ∠H + ∠L + ∠D = 360◦ , ∠H = 360◦ − (90◦ + α) − (90◦ − α) − 90◦ = 90◦.

Итак, доказано, что BL ⊥ KO, кроме того, AC перпендикулярна плоскости BB₁D₁, а значит, AC перпендикулярна любой прямой этой плоскости, в частности прямой BL. Прямая BL перпендикулярна двум пересекающимся прямым плоскости γ, следовательно, BL ⊥ γ. Что и требовалось доказать.

б) V_BAMNC = 1/3 * S_AMNC * BH = 1/3 * (MN + AC) / 2 * KO * BH.

MN = 4, AC = 8, KO найдём по теореме Пифагора как гипотенузу прямоугольного треугольника KOT, где KT || BB₁, с катетами KT = 8 и OT = TB = 2.

KO =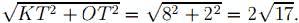 

Рассмотрим рисунок. BH найдём из подобия прямоугольных треугольников BHO и SBO (∠HBO = ∠BSO): BH/BO = SB/SO. BO = 4, SB = 16. Из подобия треугольников SBO и B₁SK с коэффициентом подобия 2 следует, что SO = 2KO = 4√17.

BH/4 = 16 / 4√17 , BH = 16 / √17 . V_BAMNC = 1/3 * (MN + AC) / 2 * KO * BH = 1/3 * (4 + 8) / 2 * 2√17 * 16/√17 = 64.

Ответ: 64.