В правильной четырёхугольной призме ABCDA1B1C1D1...

Задание:

В правильной четырёхугольной призме ABCDA₁B₁C₁D₁ на ребре AD взята точка F так, что AF : FD = 1:3.

а) Постройте сечение призмы плоскостью, проходящей через точки В₁ и F параллельно диагонали АС.

б) Найдите угол между плоскостью сечения и плоскостью основания, если
ВВ₁ — 5√6, АВ = 8.

Решение:

а) По условию ABCDA₁B₁C₁D₁ — правильная призма, это означает, что основание ABCD — квадрат и боковые грани — равные прямоугольники.

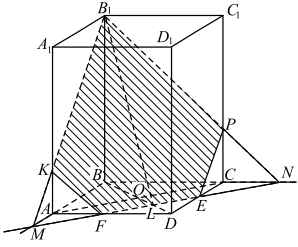
Построим сечение призмы плоскостью, проходящей через точки B₁ и F параллельно AC. В плоскости ABC через точку F проведём прямую FE, параллельную диагонали AC. Прямая FE пересекает луч BA в точке M, а луч BC в точке N. Из точки B₁ в плоскости ABB₁ и в плоскости CBB₁ проведём лучи B₁M и B₁N. Эти лучи пересекут рёбра AA1 и CC1 в точках K и P соответственно. Пятиугольник FKB₁PE — искомое сечение.

б) Найдём угол между плоскостью сечения и плоскостью основания. Плоскость сечения пересекает плоскость основания по прямой MN, MN || AC по построению, BD ⊥ AC как диагонали квадрата, MN пересекает BD в точке L, BL ⊥ MN, значит, BL ⊥ FE, BL — проекция наклонной B₁L на плоскость ABC, тогда по теореме, обрат- ной теореме о трёх перпендикулярах, B₁L ⊥ EF, следовательно, ∠BLB₁ — линейный угол двугранного угла между плоскостью сечения и плоскостью основания. В прямо- угольном треугольнике BLB₁ tg ∠BLB₁ = BB₁ / BL . Найдём BL.

ΔAOD ∼ ΔFLD по первому признаку подобия (∠O = ∠L = 90◦ , ∠D — общий). Из подобия следует AD / FD = OD / LD , LD = (FD * OD) / AD.

Найдём FD и OD. По условию AF : F D = 1 : 3, значит,

FD = 3/4 * AD = 3 * 8/4 = 6.

BD = 8√2 как диагональ квадрата, OD = 1/2 * BD = 4√2.

Тогда LD = (6 * 4√2) / 8 = 3√2.

BL = BD − LD = 8√2 − 3√2 = 5√2,

tg BLB₁ = 5√6 / 5√2 = √3,

∠BLB₁ = 60º.

Ответ: 60º.