В правильной четырёхугольной призме ABCDA1B1C1D1...

Задание:

В правильной четырёхугольной призме ABCDA₁B₁C₁D₁ на ребре CD взята точка К так, что СК = DK.
а) Постройте сечение призмы плоскостью, проходящей через точки А₁ и К параллельно диагонали BD.

б) Найдите угол между плоскостью сечения и плоскостью основания, если АА₁ = 3√3, АВ = 6√2.

Решение:

а) Так как призма правильная, то ABCD — квадрат, а боковые грани — равные прямоугольники.

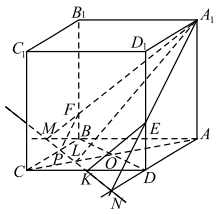
Построим сечение призмы плоскостью, проходящей через точки A₁ и K параллельно диагонали BD.

В плоскости ABC через точку K проведём прямую PK параллельно диагонали BD. Лучи AD и AB пересекают прямую P K в точках N и M соответственно. Из точки A₁ в плоскости A₁AB и в плоскости A₁AD проведём лучи A₁M и A₁N. Эти лучи пересекут рёбра B₁B и D1D в точках F и E соответственно. Многоугольник PFA₁EK — искомое сечение.

б) Найдём угол между плоскостью сечения и плоскостью основания. Плоскость сечения пересекает плоскость основания по прямой MN. MN || BD по построению, AC ⊥ BD как диагонали квадрата, MN пересекает AC в точке L, отсюда AL ⊥ MN, значит, AL ⊥ PK. Так как призма правильная, то боковые рёбра перпендикулярны плоскости основания, значит, AA₁ ⊥ ABC. AL — проекция наклонной A₁L на плоскость ABC, тогда по теореме, обратной теореме о трёх перпендикулярах, A₁L ⊥ P K. Следовательно, ∠ALA₁ — линейный угол двугранного угла между плоскостью сечения и плоскостью основания. В прямоугольном треугольнике ALA₁ tg ∠ALA₁ = AA₁/AL. Найдём AL. AC = a√2, где a — сторона квадрата, AC = 6√2 * √2 = 12. Так как CK = KD по условию и KP || BD, то по теореме Фалеса CL = OL, отсюда AL = 3/4*AC = 3/4 * 12 = 9. tg ∠ALA₁ = 3√3 / 9 = √3 / 3, ∠ALA₁ = 30◦.

Ответ: 30◦.