В равностороннем треугольнике..высота равна 45√3...
Категория: Задание 6 ЕГЭ по математике (Планиметрия)
Задание:
В равностороннем треугольнике ABC высота CH равна 45√3. Найдите AB.
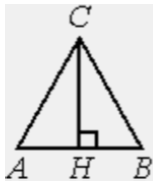
Решение:
Используем все, что дано в задаче.
1) Так как треугольник равносторонний AB = BC = AC, а уголA = углуB = углуC = 180/3 = 60°.
Угол H = 90°, так как по условию CH - высота.
2) Рассмотрим треугольник CHB.
Угол C = 180 - угол H - угол B = 180° - 90° - 60° = 30°.
Нам нужно найти сторону AB, которая по условию равна гипотенузе BC.
3) Рассмотрим тангенс угла BCH.
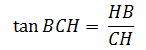, так как тангенс - это отношение противолежащего катета к прилежащему.
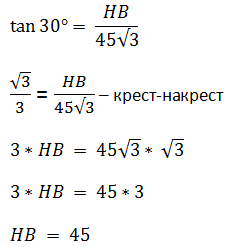
Видим на рисунке, что AB = AH + HB. Аналогичным образом находим AH = 45
AB = AH + HB = 45 + 45 = 90
Данную задачу можно решить гораздо проще, используя формулу высоты равностороннего треугольника. Посмотрим на формулу:
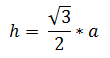, где h - высота, a - любая сторона треугольника, так как они все равны. Воспользуемся формулой, по условию h = 45√3.
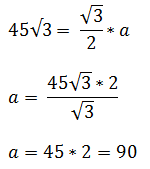
Нашли, что a = 90, значит AB = BC = AC = 90.
Ответ: 90