В трапеции KLMN боковая сторона KL перпендику...

Задание:

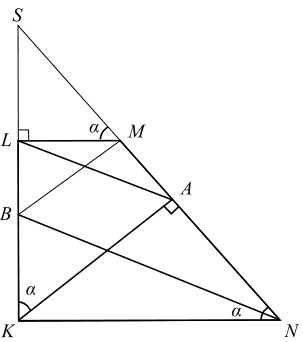
В трапеции KLMN боковая сторона KL перпендикулярна основаниям. Из точки К на сторону МN опустили перпендикуляр КА. На стороне KL отмечена точка В так, что прямые LA и BN параллельны.

а) Докажите, что прямые ВМ и MN перпендикулярны.

б) Найдите отношение LA : BN , если угол LMN равен 150°.

Решение:

а) Для доказательства перпендикулярности прямых BM и MN достаточно доказать, что BM || KA, а это выполняется в случае, если подобны треугольники SBM и SKA, то есть если справедливо равенство SB/SK = SM/SA .

Пусть ∠SML = α, тогда ∠SKA = ∠ANK = α. Из параллельности прямых LA и BN следует, что треугольники SLA и SBN подобны, значит, верно равенство SL/SB = SA/SN .

В прямоугольном треугольнике SLM SL/SM = sin α, откуда SM = SL/sin α.

В прямоугольном треугольнике SAK SA/SK = sin α,

В прямоугольном треугольнике SKN SK/SN = sin α. SK = SN * sin α.

Перемножая почленно равенства SA/SK = sin α и SK/SN = sin α, получим: SA/SN = sin² α, SA = SN sin² α. Учитывая, что SA/SN = SL/SB , имеем SL/SB = sin² α, откуда SB = SL/sin² α .

Тогда SB/SK = SL / (sin² α · SN · sin α) = SL / (sin³ α · SN) , SM/SA = SL / (sin α · SN sin² α) = SL / (sin³ α · SN). Правые части равенств равны, следовательно, SB/SK = SM/SA , значит, прямые LA и BN параллельны, и BM и MN перпендикулярны.

б) В силу подобия треугольников SML и SKN LA/BN = SL/SB. Как показано в пункте а), SL/SB = sin² α.

По условию ∠LMN = 150◦ , ∠LMN + α = 180◦ , α = 180◦ − 150◦ = 30◦ . SL/SB = sin² α = sin² 30◦ = 1/4.

Ответ: б) 1/4.