В треугольник ABC, в котором длина стороны AC меньше длины...

Задание:

В треугольник ABC, в котором длина стороны AC меньше длины стороны BC, вписана окружность с центром O. Точка B₁ симметрична точке B относительно CO. а) Докажите, что A, B, O и B₁ лежат на одной окружности. б) Найдите площадь четырёхугольника AOBB₁ , если AB = 10, AC = 6 и BC = 8

Решение:

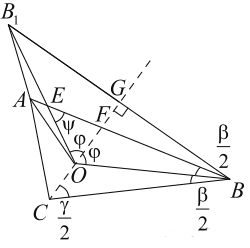
а) Пусть CO пересекает AB в точке F, OB₁ пересекает AB в точке E, CO пересекает BB₁ в точке G, а углы A, B и C соответственно α, β и γ. Покажем, что отрезок AB₁ виден из точек O и B под одним и тем же углом — это будет означать, что точки A, B₁ , B, O лежат на одной окружности. В треугольнике CGB имеем:

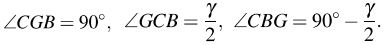
Тогда:

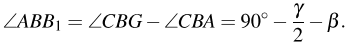
В треугольнике OGB имеем:

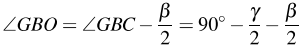, тогда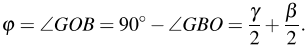

Треугольник B₁OB равнобедренный, так как GO — серединный перпендикуляр к BB₁ . Поэтому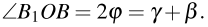 

В треугольнике ABC точка O — инцентр, поэтому 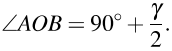Следовательно,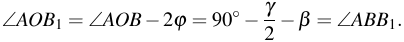 

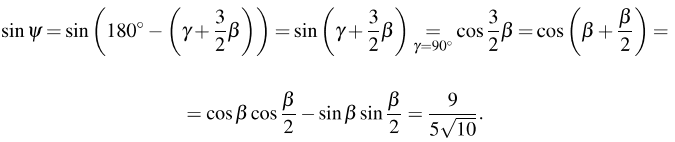
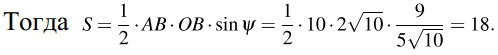
Ответ: б) 18