В треугольнике АВС проведены высоты AM и BN ...

Задание:

В треугольнике АВС проведены высоты AM и BN . На них из точек М и N опущены перпендикуляры МК и NF соответственно:

а) Докажите, что прямые KF и АВ параллельны.

б) Найдите отношение KF : АВ, если ∠АСВ = 60°.

Решение:

а) ΔANO ∼ ΔBMO по первому признаку подобия (∠ANO = ∠BMO = 90◦ , ∠AON = ∠BOM как вертикальные). Учитывая, что в подобных треугольниках пропорциональны сходственные стороны и высоты, к ним проведённые, получим AO/OB = NF/KM (1).

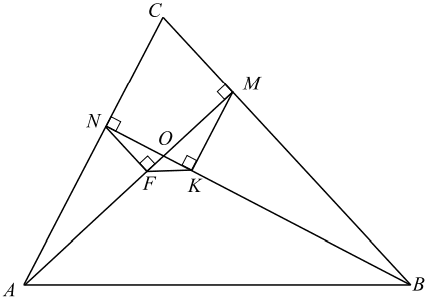
ΔNFO ∼ ΔMKO по первому признаку подобия (∠NFO = ∠MKO = 90◦ , ∠NOF = ∠MOK как вертикальные), отсюда OF/OK = NF/MK (2).

Из 1) и 2) следует, что AO/OB = OF/OK .

Следовательно, ΔAOB ∼ ΔFOK по второму признаку подобия (∠AOB — общий, AO/FO = OB/OK).

Из подобия следует ∠OAB = ∠OFK. Углы OAB и OFK соответственные при прямых AB и KF и секущей AO, следовательно, AB ‖ KF по признаку параллельности прямых.

б) В четырёхугольнике NCMO

∠MON = 360◦ − (∠N + ∠M + ∠C) = 120◦ .

В ΔMOK ∠MKO = 90◦ , ∠MOK = 60◦ как смежный с ∠MON, тогда ∠OMK = 30◦ . Пусть OK = x, OM = 2OK = 2x.

В ΔOMB ∠OMB = 90◦ , ∠MOB = 60◦ , ∠MBO = 30◦ , OB = 2OM = 4x.

По доказанному в пункте а) ΔFOK ∼ ΔAOB, значит, сходственные стороны пропорциональны: KF/AB = OK/OB = x/4x = 1/4 .

Следовательно, KF : AB = 1 : 4.

Ответ: KF : AB = 1 : 4.