В треугольнике АВС угол А равен 26°, угол В равен 82...
Категория: Задание 6 ЕГЭ по математике (Планиметрия)
Задание:
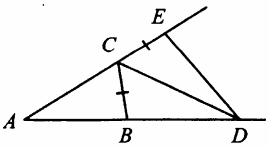
В треугольнике АВС угол А равен 26°, угол В равен 82°, CD — биссектриса внешнего угла при вершине С, причём точка D лежит на прямой АВ. На продолжении стороны АС за точку С выбрана такая точка Е, что СЕ = СВ. Найдите угол BDE. Ответ дайте в градусах.
Решение:
∠CBD = 180◦ − ∠CBA = 180◦ − 82◦ = 98◦.
Треугольники CBD и CED равны по двум сторонам и углу между ними (∠BCD = ∠ECD, так как CD — биссектриса, BC = CE по условию, CD — общая). Значит, ∠CBD = ∠CED = 98◦ . Сумма углов треугольника ADE равна 180◦ . Найдём ∠ADE = 180◦ − 26◦ − 98◦ = 56◦ .
Ответ: 56.