Вне прямоугольного треугольника АВС на его катетах АС и ВС построены...

Задание:

Вне прямоугольного треугольника АВС на его катетах АС и ВС построены квадраты ACDE и BCFG. Продолжение медианы СМ треугольника АВС пересекает прямую DF в точке N. Найдите отрезок CN, если катеты равны 1 и 4.

Решение:

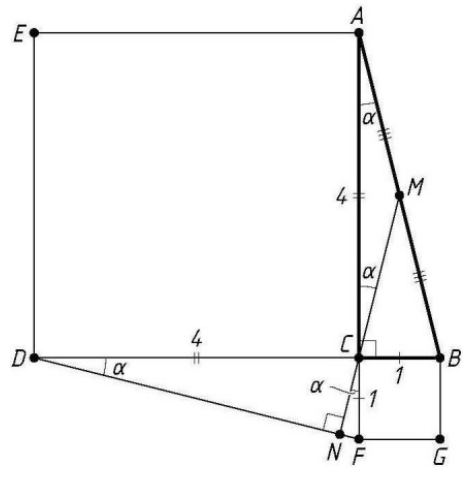
Пусть АС = 4, ВС = 1. Обозначим ∠BAC = α. Прямоугольные треугольники АВС и DFC равны по двум катетам, поэтому

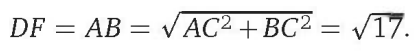
Медиана СМ прямоугольного треугольника АВС, проведённая к гипотенузе АВ, равна половине гипотенузы, поэтому

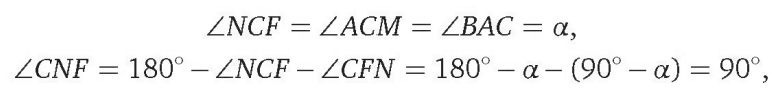
т. е. CN — высота прямоугольного треугольника CDF, проведённая из вершины прямого угла С. Поскольку CD •  CF = DF • CN (удвоенная площадь треугольника CDF),

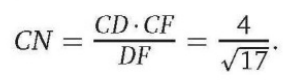
Ответ: