На рисунке изображен график дифференцируемой функции...

Задание:

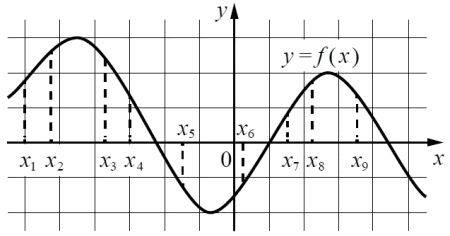
На рисунке изображен график дифференцируемой функции y = f(x). На оси абсцисс отмечены девять точек: х₁, х₂, ..., х₉. Найдите все отмеченные точки, в которых производная функции y = f(x) отрицательна. В ответ укажите количество этих точек.

Решение:

Производная отрицательна на промежутках убывания функции и положительна на промежутках её возрастания и, наконец, равна нулю в особых точках, в которых функция меняет характер своего изменения. Графически убывание характеризуется спуском линии вниз с увеличением x, возрастание – ростом линии вверх с увеличением x, смена характера изменения функции есть либо горка, либо впадинка. Основываясь лишь на таких простых замечаниях, нетрудно видеть, что нужные нам точки это x₃, x₄, x₅ и x₉ – всего 4.

Ответ: 4