На рисунке изображён график функции у = F(x) — од...

Задание:

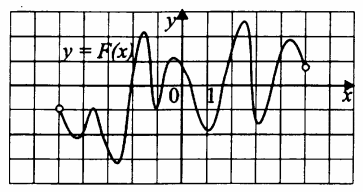
На рисунке изображён график функции у = F(x) — одной из первообразных некоторой функции f(х), определённой на интервале (- 5; 5). Пользуясь рисунком, определите количество решений уравнения f(x) = 0 на отрезке [- 3; 4].

Решение:

Согласно определению первообразной выполняется равенство: F'(x) = f(x). Поэтому уравнение f(x) = 0 можно записать в виде F'(x) = 0. Так как на рисунке изображён график функции y = F(x), то надо найти те точки промежутка [−3; 4], в которых производная функции F(x) равна нулю. Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 7 (четыре точки минимума и три точки максимума).

Ответ: 7.