На рисунке изображён график у = f'(x )— производной...

Задание:

На рисунке изображён график у = f '(x )— производной функции f(x). Найдите абсциссу точки, в которой касательная к графику функции у = f(x ) параллельна оси абсцисс или совпадает с ней.

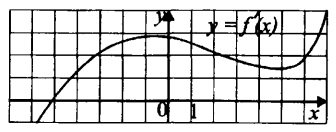
Решение:

Пусть x₀ — абсцисса точки, в которой касательная к графику функции y = f(x) параллельна оси абсцисс или совпадает с ней. Тогда значение производной y = f '(x) в точке x₀ равно 0, так как угловой коэффициент оси абсцисс y = 0 равен 0.

Но из графика видно, что f '(x) = 0 в единственной точке x₀ = −5.

Действительно, прямая y = 0 пересекает график функции
y = f '(x) в единственной точке (−5; 0), абсцисса которой равна −5.

Ответ: −5.